유클리드 호제법의 개념과 Java 코드

유클리드 호제법이란? 

2개의 자연수의 최대공약수를 구하는 알고리즘의 하나이다.

유클리드(Euclid)에 의해 기원전 300년경에 발견된 가장 오래된 알고리즘이다.

(호제법이란 말은 두 수가 서로(互) 상대방 수를 나누어(除)서 결국 원하는 수를 얻는 알고리즘을 말한다.)

 

 

유클리드 호제법을 알아보기 전, 어렸을적 배운 최대 공약수와 최소 공배수를 구하는 방법을 살펴보자.

---

소인수 분해를 이용해 최대 공약수, 최소 공배수 구하기 (중요x)

 

최대공약수 (Greatest Common Divisor)

두 자연수의 공통된 약수 중 가장 큰 수를 의미하며, GCD 라고 한다.

 

 

 

최소공배수 (Least Commn Multiple) 

두 자연수의 공통된 배수 중 가장 작은 수를 의미하며, LCM 라고 한다.

 

 

 

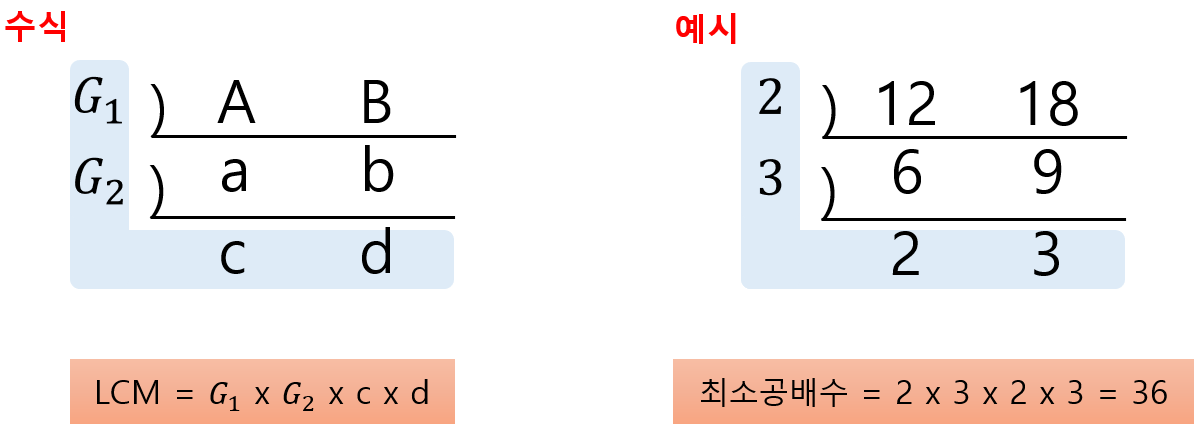
소인수 분해를 이용할 경우, 시간복잡도는 O(N) 으로 시간이 매우 많이 걸려 비효율적이다.

---

유클리드 호제법을 이용해 최대 공약수, 최소 공배수 구하기

1. 큰 수를 작은 수로 나누어, 나머지를 구한다.

2. 나눴던 수와 나머지를 나누어, 나머지를 구한다.

3. 나눴던 수와 나머지를 나누어, 나머지를 또 구한다.

4. 위 과정을 나머지가 0 이 될 때까지 반복 한다.

유클리드 호제법을 이용할 경우, 시간복잡도는 O(logN)으로 시간에 효율적인 알고리즘이다.

 

유클리드 호제법 알고리즘의 Java 코드는 다음과 같다.

public class Main {

    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        int a = sc.nextInt();       // 입력1
        int b = sc.nextInt();       // 입력2

        // 유클리드 호제법
        int gcd = GCD(a, b);
        int lcm = LCM(a, b, gcd);
        
        // 출력
        System.out.println("최대공약수 : " + gcd);
        System.out.println("최소공배수 : " + lcm);
    }

    /**
     * 최대 공약수 (GCD)
     */
    public static int GCD(int a, int b){
        if(b == 0) return a;
        else return GCD(b, a % b);
    }

    /**
     * 최소 공배수 (LCM)
     */
    public static int LCM(int a, int b, int gcd){
        return a * b / gcd;
    }
}